PROJECTILE

 http://web.ncf.ca/ch865/graphics/Projectile1a.jpeg

 

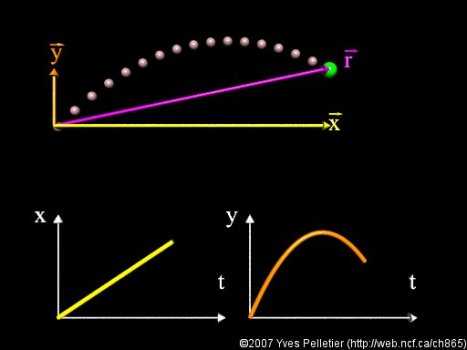
Suppose an object is moving horizontally at the same time it is falling. Does the horizontal motion affect the vertical motion, or vice versa? It turns out that the two motions, horizontal and vertical, are quiet dependent to each other. This behavior is called projectile motion.

The path trace by the projectile Is called trajectory. Because of the force of gravity, the bullet begins to fall the instant it leaves the rifle. For this reason, rifle sights are so adjusted that the rifle is aimed at a point above the target, while the line of sight is in line in the target. The longer the range is, the more time the bullet has to fall. The longer the range, therefore, the more the rare sight must be elevated.

 Sample: A bullet is fired horizontally with an initial velocity of          300m/s from the top of a tower, 40 meters high. How far from the base, of the tower will the bullet hit the ground?

 Sol’n

S=1/2 gt2

40 m=1/2(9.8m/s2) t2

t=2.86 s

S=vavex t

S=300m/s x 2.86s

S= 857.14m

 

Sample Problems

A shell being fired into enemy territory is an excellent example of projectile motion in action.  The controller in charge of targeting the enemy must use radar technology to take an electronic reading of the distance.  He must then use the velocity of the shell (which is a constant), and set the angle of the barrel using the distance desired.  He must take into account the force of gravity as a negative acceleration and apply his knowledge of downwards acceleration due to gravity in order to succeed in hitting his target.  This is an example of projectile motion, which applies the concepts of Newton’s First Law of motion and the Acceleration due to Gravity concepts.

 
Example:  George hits a golf ball horizontally off a 25.0 m high cliff with a speed of 45 m/s.  How far from the base of the cliff will the golf ball strike the ground?
Find time:
Vertical:            d =vi (t) + (1/2)(a)(t2)
                        25 = 0 (t) + (1/2)(9.8)(t2)
                        25 = 4.9 (t2)
                        t2 = 25/4.9
                        t2 = 5.10
                        t = 2.26 sec
Find horizontal distance:
Horizontal:       d =vi (t) + (1/2)(a)(t2)
                      d = (45) (2.26) + (1/2)(0)(t2)
                      d = 45 x 2.2
                      d = 102
The ball strikes the ground 102 m from the base of the cliff.

Problems Reference:

http://www.physics247.com/physics-tutorial/projectile-motion.shtml